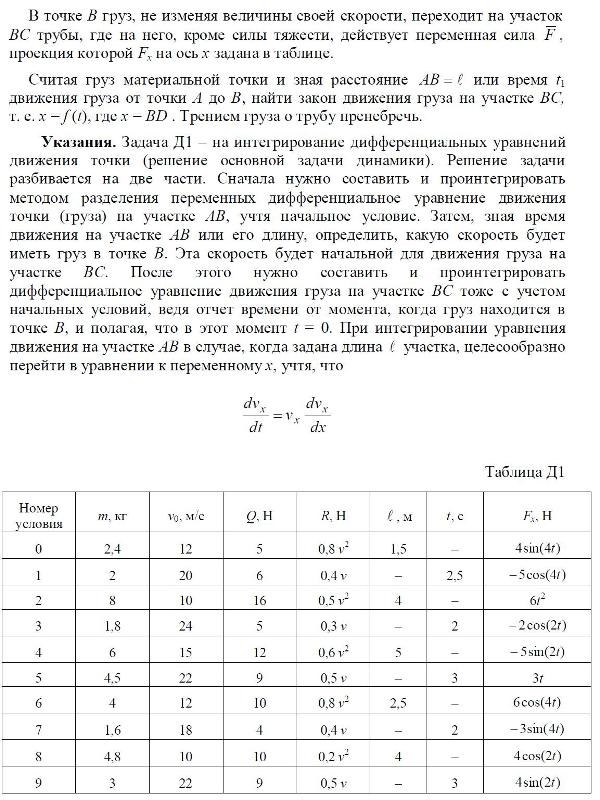
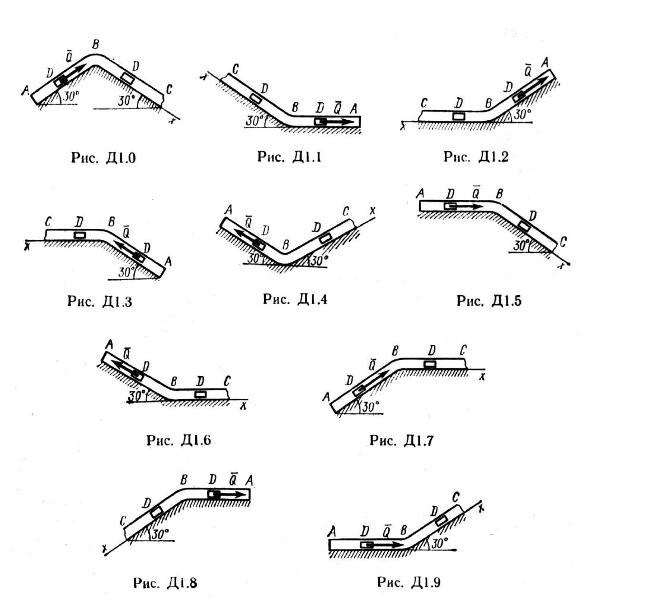
Внимание!

Номер рисунка выбирается по последней цифре варианта, а номер условия в таблице - по предпоследней  цифре варианта.

Например: вариант 27

номер схемы - 7

номер условия - 2 

Перейти к решенным задачам 

Задача Д1

Груз D массой т, получив в точке А начальную скорость v₀, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 — Д1.9, табл. Д1). На участке АВ на груз, кроме силы тяжести, действуют постоянная сила  (ее направление показано на рисунках) и сила сопротивлении среды , зависящая от скорости v груза (направлена против  движения).

В точке В груз, не изменяя величины своей скорости, переходит на участок ВС трубы, где на него, кроме силы тяжести, действует переменная сила , проекция которой F_x на ось x задана в таблице.

Считая груз материальной точки и зная расстояние  или время t₁ движения груза oт точки А до В, найти закон движения груза на участ­ке ВС,     т. е. х = f (t), где х = ВD . Трением груза о трубу пренебречь.

Указания. Задача Д1 – на интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке АВ, учтя начальное условие. Затем, зная время движения на участке АВ или его длину, определить, какую скорость будет иметь груз в точке В. Эта скорость будет начальной для движения груза на участке ВС. После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке ВС тоже с учетом начальных условий, ведя отчет времени от момента, когда груз находится в точке В, и полагая, что в этот момент t = 0. При интегрировании уравнения движения на участке АВ в случае, когда задана длина  участка, целесообразно перейти в уравнении к переменному х, учтя, что...

ПЕРЕЙТИ К РЕШЕННЫМ ЗАДАЧАМ  ТАРГ 1983 г.